Posted: 2021-08-12
This post is adapted from my notes for a talk I gave at Practice 2018 called “Word Breakers: Rewordable and the raw material of word games”. This version has been lightly updated with clarifications and references. (I also gave it a new title, to better reflect the talk’s contents.) Some portions of this talk are derived from a different talk I gave at the Independent Games Summit at GDC 2018, which itself was based on a Medium post from 2016.
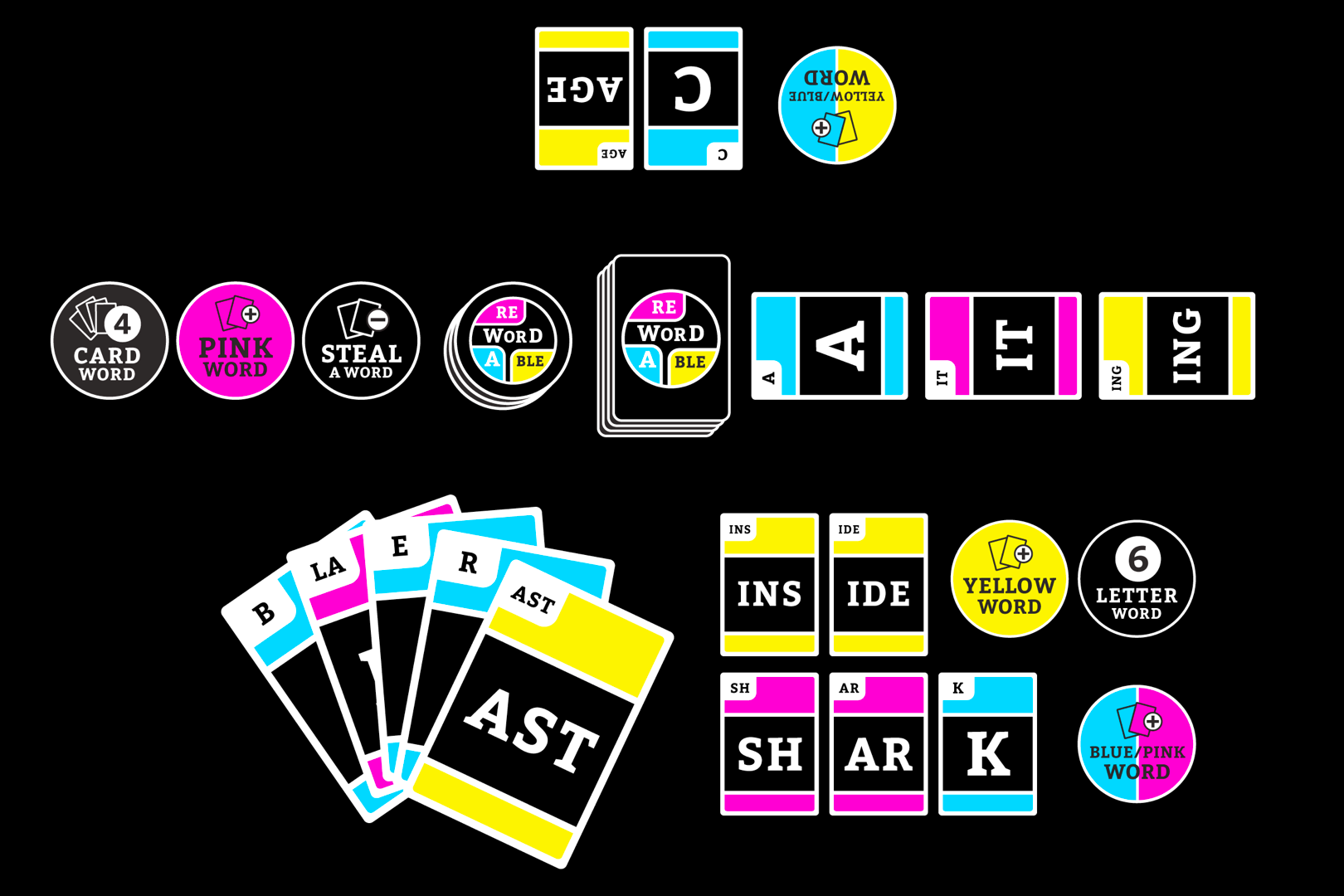
I’m going to be talking about Rewordable, which is a game I co-designed with Adam Simon and Tim Szetela. Rewordable is a word-building card game, where each card has a sequence of one, two, or three letters. On each turn, you form a word from cards currently in play or in your hand. There are also reward tokens that you can earn from the words that you make each turn.
We were in the NYU Game Center’s Incubator program in 2016 and were funded on Kickstarter that same year. Clarkson Potter, an imprint of Penguin Random House, published the game last August.
This talk is going to be about my contribution to the design process—in particular, I’m going to walk you through the computational analysis I did and some of the tools I made to make Rewordable possible, and how that process fed into playtesting to produce the game that you all know and love.
But the talk is also a bit about me trying to contextualize the work I did on Rewordable as part of a larger set of concerns that I have as a poet and artist. The words you use in your bio to describe yourself—like “Allison Parrish is a poet and programmer” etc. are usually sort of aspirational, like “I am introducing myself to you in this way so that you will understand me as belonging to the aforementioned category.” I put “game designer” in my bio, but in this case it’s less of an aspiration that it is an empirical observation about myself. I have co-designed and published a game; I am speaking at a game design conference; I guess I must be a game designer.
I do love games, but my real interest is language—in how language is turned into systems, especially computational systems, and how the process and artifacts of such systems can be challenged and repurposed for creative and poetic ends. In other words I just really want to use a computer to ugh punch language in the face.
So this talk is about the practice of game design, both in the sense of how I helped to design this particular game, but also about how game design is, for me, a part of a larger artistic practice.
A few months ago the social media team for our publisher posted a photo of Rewordable to their Instagram and this was the caption:
I should make it clear that I trust the marketing and sales teams at our publisher completely, and intellectually I understand why they might think that it makes sense to draw a comparison between our game and two wildly successful games that have sort of similar premises and materiality. And I understand how it’s my failure as a designer that the game I made does not suggest the similarities and differences that I hope it will ultimately suggest.
Regardless, this caption made me sad. I don’t especially like Scrabble or Bananagrams, and believe that Rewordable is very clearly different from (and better than) both of them. I’m going to explain to you why it made me sad.
First of all, Bananagrams is just letter tiles in a fanciful bag! That’s all it is! Bananagrams is already Scrabble meets Bananagrams.
But second, one of the reasons that Tim and Adam and I made the game in the first place was because of the shortcomings of word games like Scrabble—which seems like it’s a game about language, but is actually a game about memorizing short and obscure dictionary words and lording this knowledge over your friends and family. We actually started working on Rewordable in 2008, as the final project for Frank Lantz’s game design class at ITP. We wanted to make a word game where you can win without turning into a jerk.
Later in the talk I’m going to go a bit more into (a) why I think this it’s the case that good Scrabble play necessarily manufactures jerks and (b) why I’ve sort of had it with Scrabble and games like it as a system from an aesthetic standpoint.
But first I want to talk about our strategy for designing Rewordable so that it doesn’t “feel like” Scrabble. Our strategy, essentially, was to make a word game where you play with sequences of letters, instead of individual letters, to encourage the formation of longer, less obscure words—a game that is less about memorization and persnickety rules of spelling than it is about playful word building.
As the programmer and linguist on the design team, figuring out which sequences of letters should be on the cards fell to me. I wanted word formation in Rewordable to feel natural and a bit magical: the words should seem to fall out of the deck, almost unbidden. So it was really important to pick the right sequences to include.
More specifically, if you’re using the 26 letters of the English alphabet, there are about 18000 possible sequences of three letters or less. My task was to identify which of these sequences to print on cards and include in the game.
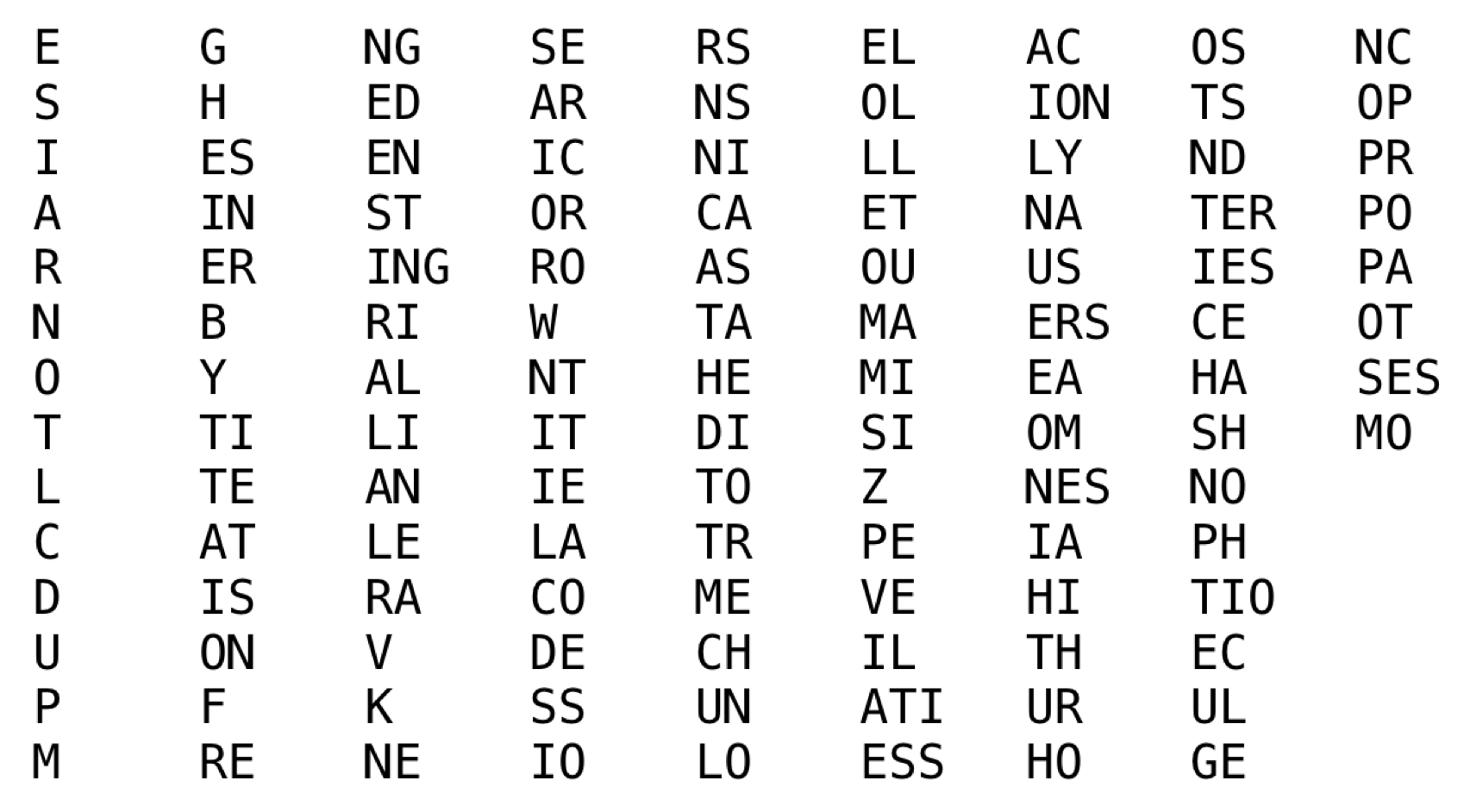
My first instinct was to analyze a representative list of English words and figure out which of those 18000 sequences were most common. I figured the most common sequences would also be the best sequences! Here’s the list of the 120 most common sequences of 1, 2, and 3 letters in English. For the original Rewordable deck, we used a list of cards very similar to this one, padding it out with more single letter cards to form a deck of 160 total.
Here’s a picture of the deck we turned in for our final in Frank’s class. Note the top card in the hand:
When we actually played games with this deck, it turned out that some of the cards were impossible to use. These cards would get stuck in people’s hands until the end of the game. The biggest offenders were TIO and ATI. Both of these are very common sequences of letters in English words (think of words like “information” and “computation”), but they’re impossible to use to form a word unless you have a bunch of other letters to play with them, like A or O or N.
So… not ideal.
Fast forward eight years later, when Rewordable was accepted to the NYU Game Center Incubator program. I decided to take the opportunity to actually figure out why sequences like ATI and TIO don’t work, and how to make a new deck with cards that didn’t have the same problem. I went down a couple of different paths. I made a matrix of sequence co-occurrence to find the cards that occurred most frequently with other sequences in an attempt to find the “friendliest” sequences:
In an attempt to find the most versatile sequences, I made these histograms of where in words particular sequences fell, relative to the beginning and endings of those words. The sequence TE is spread fairly evenly across the words it occurs in, and so—by this line of reasoning—it could be a good card to include.
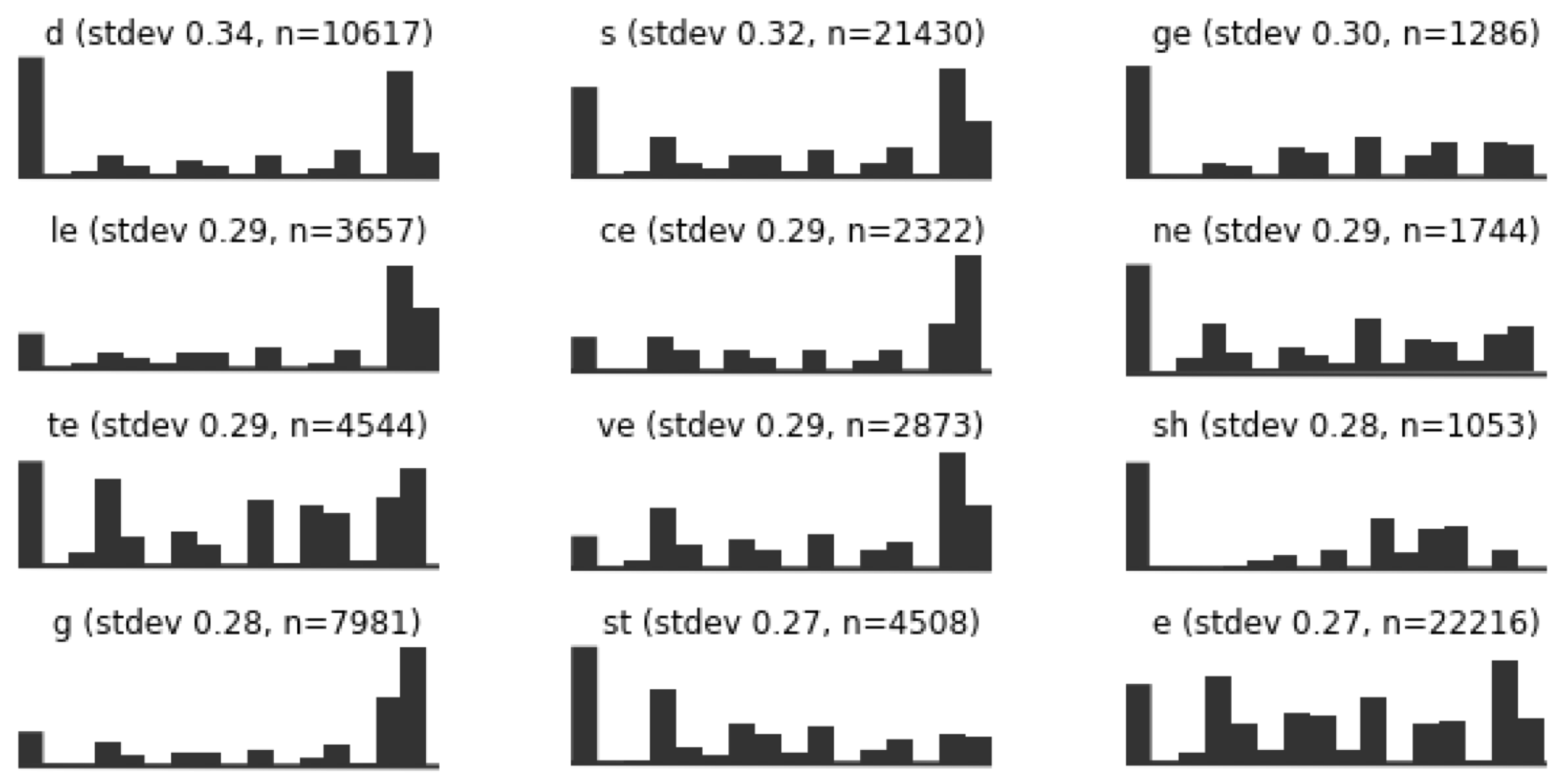
Here are some of the sequences with the lowest variance. so even though DIS is a relatively frequent sequence (1953 occurrences in the corpus), it really only ever appears at the beginning of words. So not an ideal card for the deck, maybe?
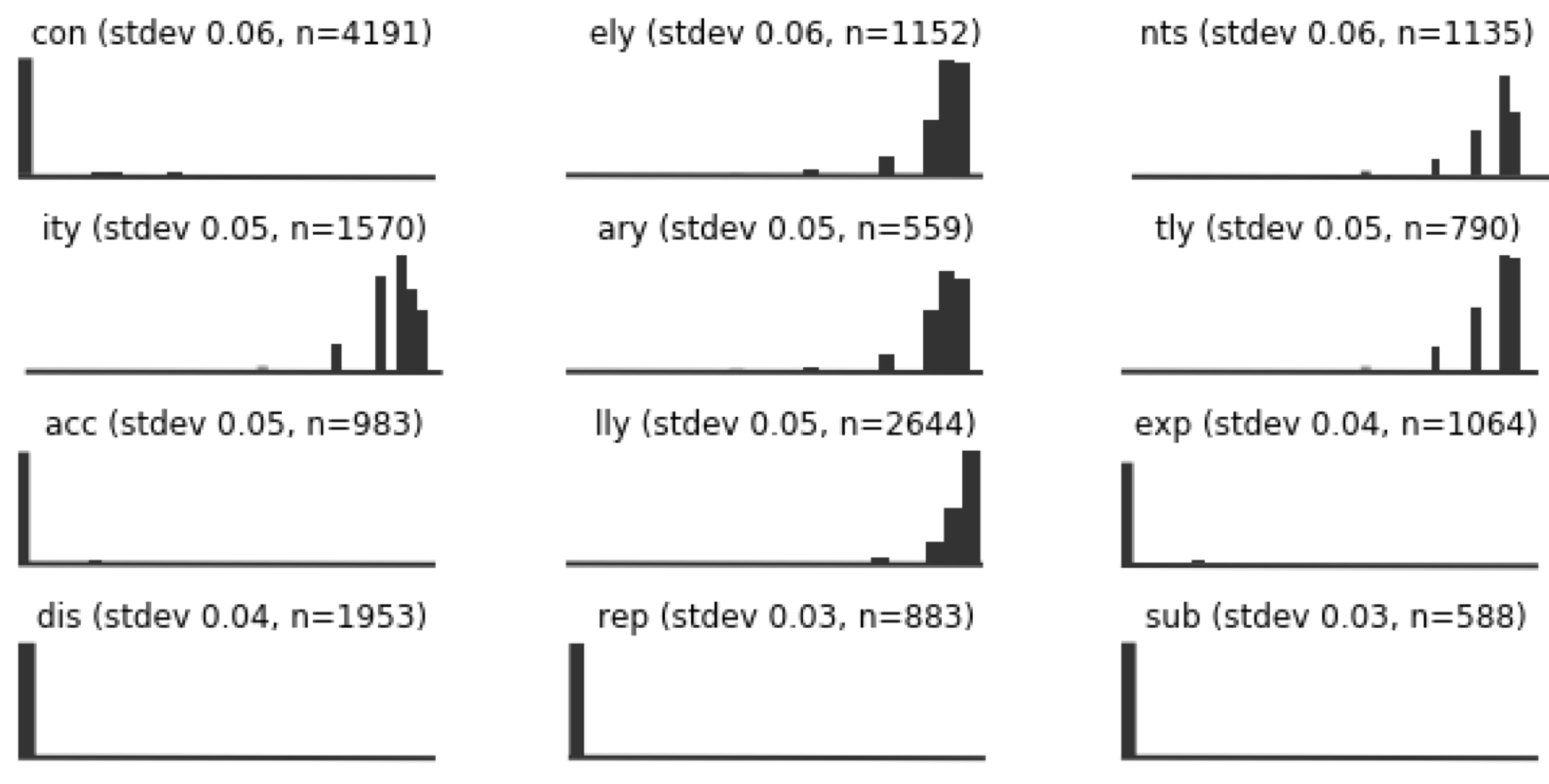
This was all very interesting, but these methodologies were still ending up with decks that included sequences like ATI and TIO—which I empirically knew were no good. I was getting valuable insights, I still wasn’t producing viable decks.
While I was lost in these dry statistical analyses, Tim was actually at the Game Center, playtesting the game with anyone who would sit down with him for twenty minutes.
In particular, Tim had been playtesting a version of the deck with only 64 cards, instead of 160, which he called Chipmunk. The idea was that a 64-card deck would be both cheaper to produce and faster to play. I was super skeptical about this deck at first, mainly because Tim decided on the deck composition by the seat of his pants and not based on my painstaking statistical analyses. But this version of the deck was AMAZING. rounds moved really quickly, and no one had to pass their turn. it was a revelation.
After playing a round with Chipmunk, I realized that the smaller deck made the game better: fewer possible combinations meant fewer possible incompatibilities between cards. And that was the key insight: I shouldn’t be looking for the best list of individual sequences according to whatever absolute statistical metric, but the set of sequences that worked best together.
We eventually decided that Chipmunk was a bit too small, since with only 64 cards, the same words would come up in basically every round. The deck was fast, but it wasn’t expressive. We decided the optimal deck size would probably be somewhere around 120 cards. The task now was to come up with a program to generate not just the best sequences but the best decks.
Computationally speaking, evaluating entire decks is much more difficult than evaluating individual sequences. There are only around eighteen thousand possible one-, two- or three-letter sequences. But there are this many possible 120-card decks using those same eighteen thousand sequences:
Any code to evaluate this many decks would keep your laptop busy until the heat death of the universe.
But we had to ship to our Kickstarter backers in April 2017, which—as you’ll recall—was well before the heat-death of the universe. I needed to find a manageable way to navigate this possibility space, so I made a rudimentary genetic algorithm that would generate decks at random, simulate play with those decks a few hundred times, assign a score to each deck based on its simulated performance, and feed the best-scoring decks back into the pool. Here’s a typical result from this process after a few generations:
I still think this is a good way to solve the problem, but due to time constraints I wasn’t able to really tune the performance of the genetic algorithm, so the program wasn’t making a dent in the possibility space. I realized, however, that the part of the program that I wrote to simulate rounds of play was valuable on its own: it was essentially a way of playtesting the game automatically, and at scale.
Tim, of course, could only do one human playtest at a time, which limited his ability to make well-motivated decisions about how to change the deck.
So I made a standalone version of the function that simulated play, called evaluatedeck.py, and packaged it up for Tim to use between playtests. He could do a playtest, propose a change to deck composition, and then run the program with the new deck to see how it would perform, getting thousands of rounds of insight without having to organize thousands of rounds of playtesting. The final workflow looked something like this: an idea about deck composition goes into playtesting; tweaks to the deck are evaluated with the program, which can then guide further tweaks; eventually, the whole thing gets formalized as a new deck and playtested again.
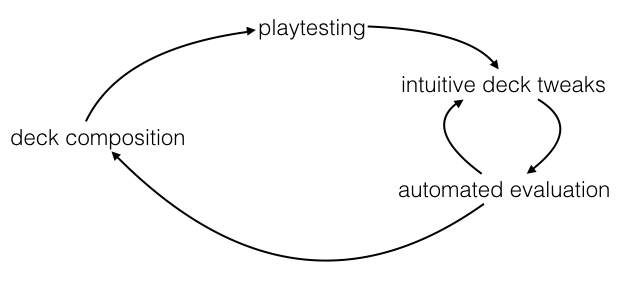This strategy worked out great! Here are some screenshots from the output of the tool, based on a version of the deck from 2016 called Pelican. Basically, you give the program a list of cards in the deck, and it spits out a bunch of different lists and statistics. For example:
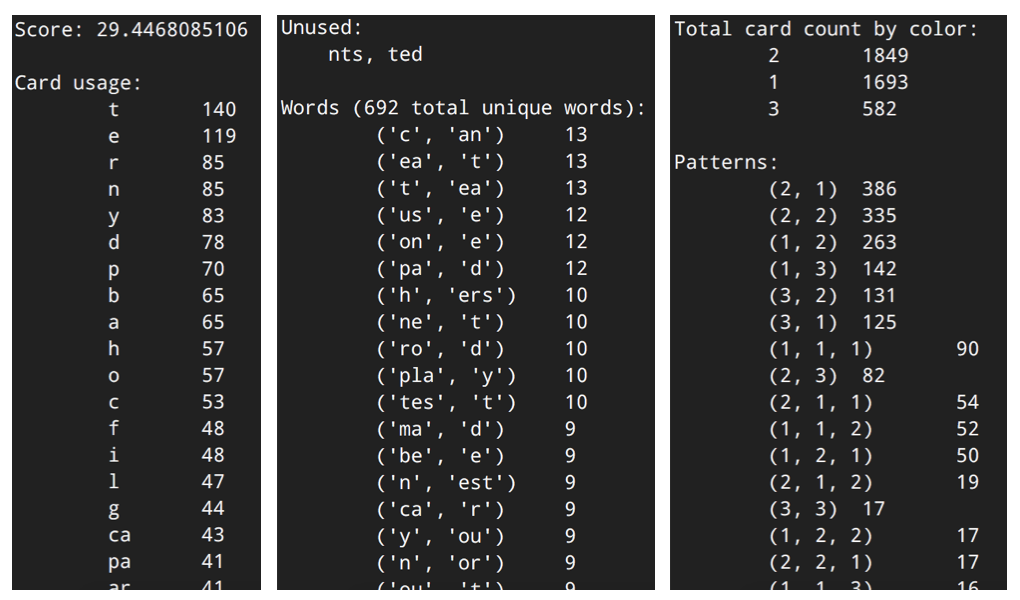The program shows how often each sequence was used, along with a list of sequences that weren’t used at all in any round of simulated play. If you’re wondering why Rewordable doesn’t have single-card J, X, Q, or Z cards, it’s because this program showed us that more often than not they just didn’t get used. So we got rid of ’em.
The program also shows a list of all the words formed during the simulated rounds. This gives us an idea of what words are likely to show up when players actually play the game. It also helps us make sure that cards that occur frequently are, in fact, being used in different words, not just in similar words over and over.
The program also shows how often cards with one, two and three letters are used, along with the patterns of different length sequences. So for example, words with one three-letter card followed by one two-letter card happened 131 times in with deck. This part of the output was vital in balancing Rewordable’s “reward token” mechanic—for example, we specifically designed the deck to have lots of words that are made of two cards with 3 letters a piece, to make it easier to win one of the reward tokens.
Here’s a picture of all 120 cards in the final deck we shipped:
The engineer who lives in my brain would have been happier if I’d been able to come up with a 100%-algorithmic solution to the problem of deck composition. But the hybrid approach that we used really worked—statistical experimentation, combined with real-life playtesting, informed by simulation—and I think we ended up with a deck that is super fun to play.
So that’s some background on how the design of Rewordable proceeded. In the remainder of this talk, I’m going to reflect on what exactly I find so objectionable about word games like Scrabble. Looking back at the design process of Rewordable—and familiarizing myself with the history of spelling games—has helped me to formulate what I’m calling “the unstated axiom of spelling game design for some reason”:
The level of skill associated with forming a word is a function of the level of skill needed to make use of the letters comprising the word
This is the axiom that results in the word (e.g.) QUICK being worth 20 points in Scrabble (Q=10 + U=1 + I=1 + C=3 + K=5), while the word ANNIHILATION is only worth 15 (all letters worth one point except H, worth 4). This axiom looks so commonsense, and it’s so deeply engrained in the spelling games that we love and grew up with, that it’s hard to even think about what could be wrong with it. I hope to show that the axiom, no matter how “common-sense,” is actually what makes Scrabble unpleasant to play, and also unnecessarily limits the scope of spelling game design.
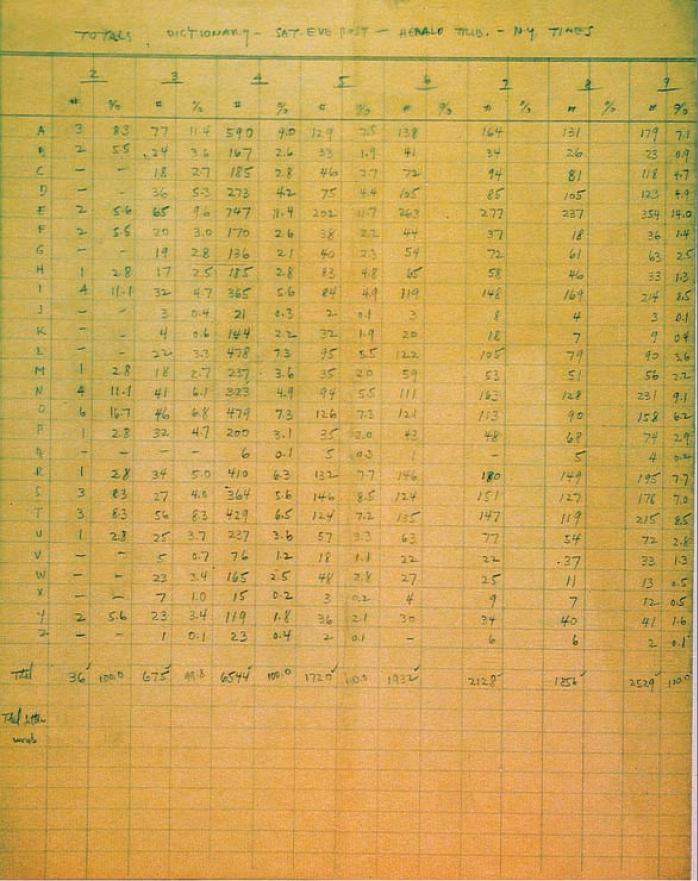
Scrabble is the game that most directly expresses this axiom, and in fact Alfred Butts, the inventor of Scrabble, formulated the ideas behind it very succinctly when designing Scrabble (and a number of predecessors). Butts used letter frequencies to determine Scrabble’s tile distribution:
“It follows that word games should be played not with a jumble of letters… but with a mixture so proportioned that the individual letters will occur in the same frequency as they do in normal word formation.”1
And then used those same frequencies to assign point values to the use of those letters:
“Butts… assigned values to letters roughly corresponding with their frequency […] but there’s little about how he settled on the point values […]. My conclusion: Butts coupled intuition with direct observation of the game in action—he tested it on his wife and their friends—to arrive at values that he felt balanced equity and volatility.2
That combination—letters are the units, letters appear in accordance with their statistical frequency, letter score inversely related to frequency—exactly recapitulates the axiom.
I think in the popular imagination, there’s this idea that Alfred Butts sat down with a copy of the New York Times and a ledger sheet in 1933 and singlehandedly invented quantitative linguistics, but these ideas behind the axiom were actually already a part of games at the time. Consider, for example, this set of alphabet blocks manufactured in the mid-1800s that comes in a set of twenty cubes, each of which has several letters on their sides. The stated goal of these blocks is to make it possible to spell “all words in general use,” including words that have repeated letters.3
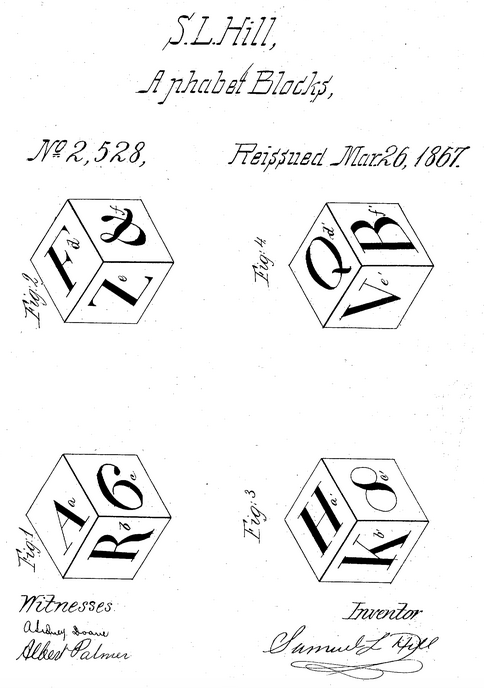
I looked at an instruction sheet4 for S. L. Hill’s alphabet blocks and pulled out the letter frequencies. Here’s a graph showing the counts for each letter:
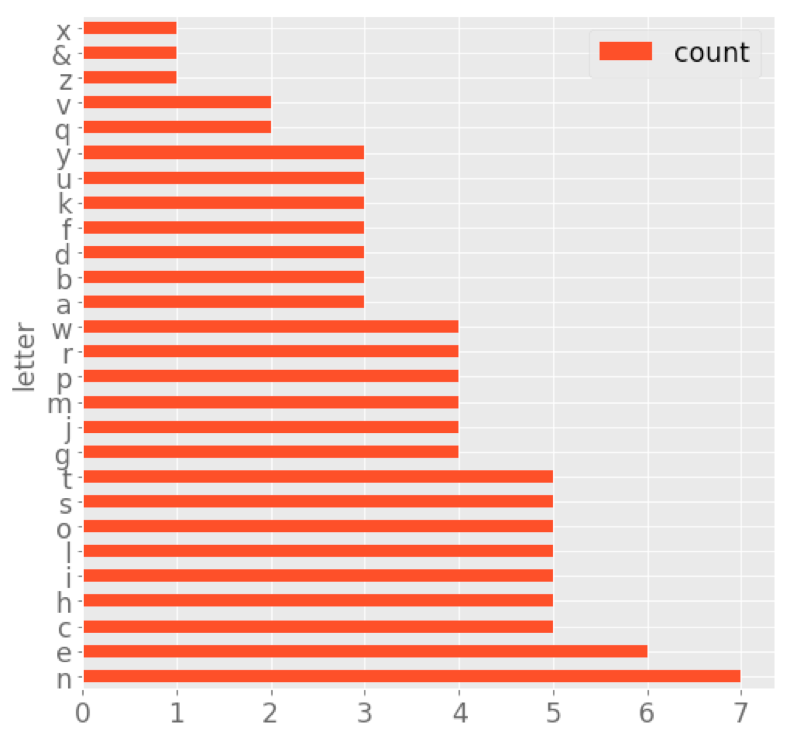
This distribution seems to… roughly follow English letter frequencies, with some weird outliers (five Cs, but only three As, way too many Js, not enough Zs to spell “pizza,” etc.). I wonder if Hill simply invented this distribution from his intuition, or if he actually did some counting, or if he had some other source. Regardless of how systematic Hill was in inventing his letter distribution, this is hardly a “jumble of letters” either. In fact, if you look at other toys and games that use letters as units at the time, you’ll find many of them have similar distributions.
Likewise, the idea of assigning scores to letters based on their perceived difficulty was already a part of several games. For example, consider “Logomachy” (/loʊˈɡɑ.mə.ki/), an “Anagrams” variant from 1874 that already incorporates this idea—Z and Q are “double prizes” while X and K are “prizes” (presumably acting as bonuses or multipliers on scores for words that were formed with them).5
Alfred Butts himself was inspired to incorporate letter frequencies in his game by reading this passage6 from Poe’s 1843 story “The Gold-Bug,”7 in which the character William Legrand describes deciphering a simple substitution cipher using English letter frequencies. This story helped to popularize cryptograms and was among Poe’s most widest-read works during his lifetime.8 In a substitution cipher, a secret message is “encoded” by systematically replacing every letter with another letter. You can decipher the message (as the protagonist of “The Gold-Bug” does) by assigning letters in the ciphertext to decoded letters based on correspondences between their relative frequencies.
But even before that, in the 9th century CE, the mathematician Al-Kindi, born in Baghdad, had more or less completely formulated the idea of solving letter substitution ciphers through letter frequency analysis:
One way to solve an encrypted message, if we know its [original] language, is to find a [different clear] text of the same language… and then we count [the occurrences of] each letter of it. […] Then we look at the cryptogram we want to solve and we also classify its symbols. We find the most occurring symbol and change it to the form of the [most common] letter [of the cleartext sample], the next most common symbol is changed to the [second most common]… and so on, until we account for all the symbols of the cryptogram…9
So there’s a good reason that the axiom I’ve identified is an unspoken part of the zeitgeist. The core idea underlying it—that letter frequency is inversely related to legibility—had been around for a thousand years, if not longer.
So here’s my contention. In designing Scrabble to use letter frequency, Butts believed he was optimizing for words that would be easier to spell. But because he assigned higher score values to rarer letters, he was ended up optimizing for words that are more difficult to decipher. We can think about this in terms of a statistical distribution. Below is a chart showing typical frequencies of individual letters English prose:
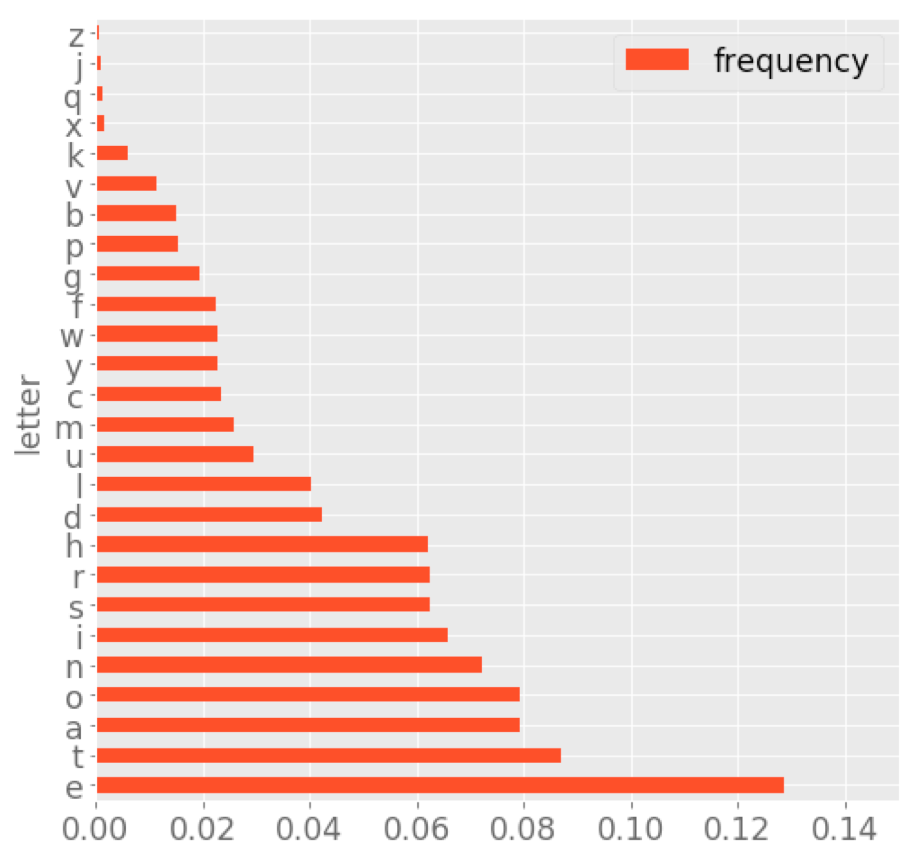
You can see that this distribution is not uniform: some letters are more frequent than others. A text encoded with a simple substitution cipher that had a similar distribution would be easy to decrypt, because you’d be able to make reasonable and accurate guesses about which letters in the clear text and ciphertext correspond to one another.
Below is an “artist’s rendering” of a hypothetical text in which the distribution is uniform—i.e., no one letter is more frequent than any other:
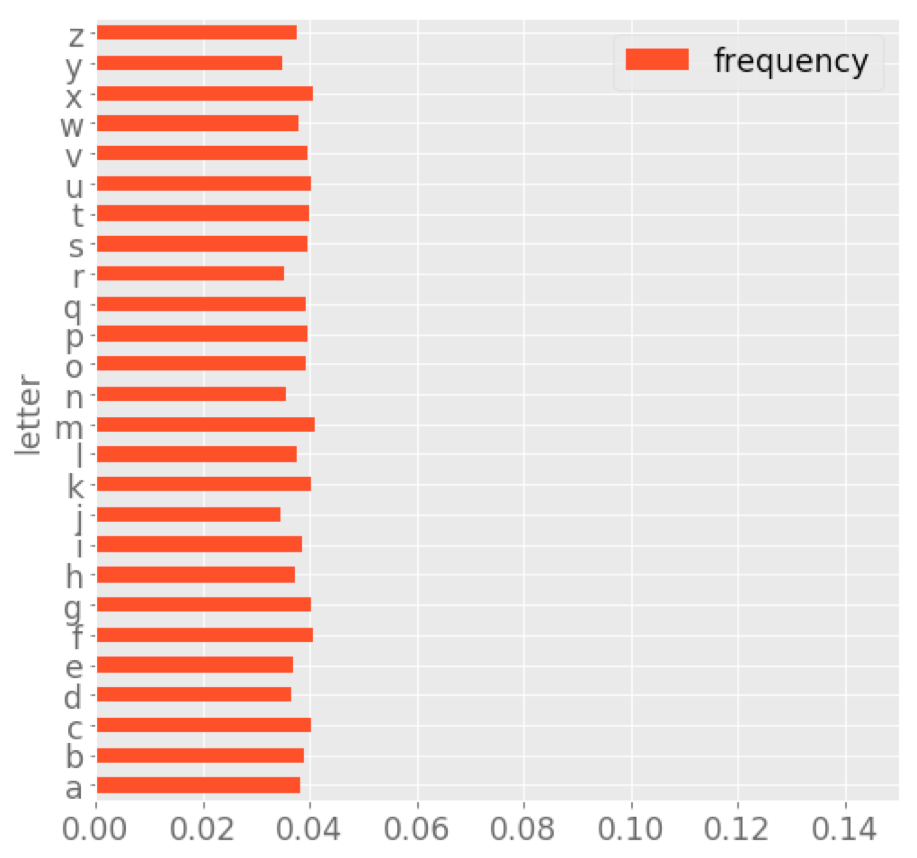
A ciphertext that had this distribution would be difficult to decipher, because ordering the letters by frequency would reveal no useful correspondences with letters in the clear text. Likewise, in Scrabble, the essential goal is to minimize the number of high-frequency/low-score letters you use, and maximize the number of low-frequency/high-score letters. This is the reason that high-scoring Scrabble words tend to be words that (paradoxically) resemble “jumbles of letters”: your qophs, zas and jeezes.
Returning to the axiom:
the level of skill associated with forming a word is a function of the level of skill needed to make use of the letters comprising the word
“Maximize the extent to which your letters correspond to a uniform distribution” is a succinct way of phrasing this axiom. In my opinion, this is the core part of the reason that playing Scrabble well makes you a jerk: to compete in Scrabble, you have to be working mentally from a list of words that meet particular statistical characteristics of letter-by-letter rarity, which tend to be obscure words with unintuitive spellings that must be learned by rote.
This property of Scrabble play is discouraging for players who approach Scrabble hoping to use a other parts of their language competency, e.g., their internal sense of which letters are likely to follow which other letters. Rewordable is addressed to these players. It uses pre-baked sequences, and doesn’t focus exclusively on frequency of occurrence as a criterion for inclusion in the game. Additionally, in Rewordable, the score you get for playing a card is not based on the rarity of letters that the card contains.
“It follows that word games should be played not with a jumble of letters… but with a mixture so proportioned that the individual letters will occur in the same frequency as they do in normal word formation.”
I want to return to the Alfred Butts quote from earlier and examine another unstated presupposition contained therein: “individual letters.” We sort of take it for granted that spelling games will use letters as their unit. But why should this be the case?
Letters are units that are unique to alphabets, a kind of writing system in which each symbol corresponds to an individual sound. Most writing systems in the world are not alphabets. There are many other kinds of writing systems in the world, each of which relates glyph to language in different ways. For example:
The association of a writing system and a language is historically contingent, not inherent to the language itself. In fact, many languages have, over the course of their histories, been written with different types of writing systems. English and the alphabet are not the same thing—English could be written in a different way.
But a weird thing happened in the history of Western thought: for many writers in Europe who just happened to inherit languages (like Latin) whose most common written form was alphabetical, the alphabet became a sacred thing that stood in for language. For example, consider this quotation from the writings of John Scotus Erigena, ninth century Irish monk and neoplatonist:
“Motion terminates at no other end save its own beginning, in order to cease and rest in it… [Likewise], grammar begins with the letter, from which all writing is derived and into which it is all resolved”10
This formulation inverts the contemporary structuralist understanding of writing, in which language is recorded by means of making marks on the page, the form of which is arbitrary. For Erigena, letters themselves are the deep structure of language, from which language springs—not the other way around.
But why stop there? Perhaps the world itself can best be understood as but a reflection of the letters of the alphabet. John Amos Comenius’ Orbis Sensualium Pictus, a popular textbook for children from the 1600s, includes the alphabet chart below, which builds a taxonomy of animal life using the letters of the alphabet.
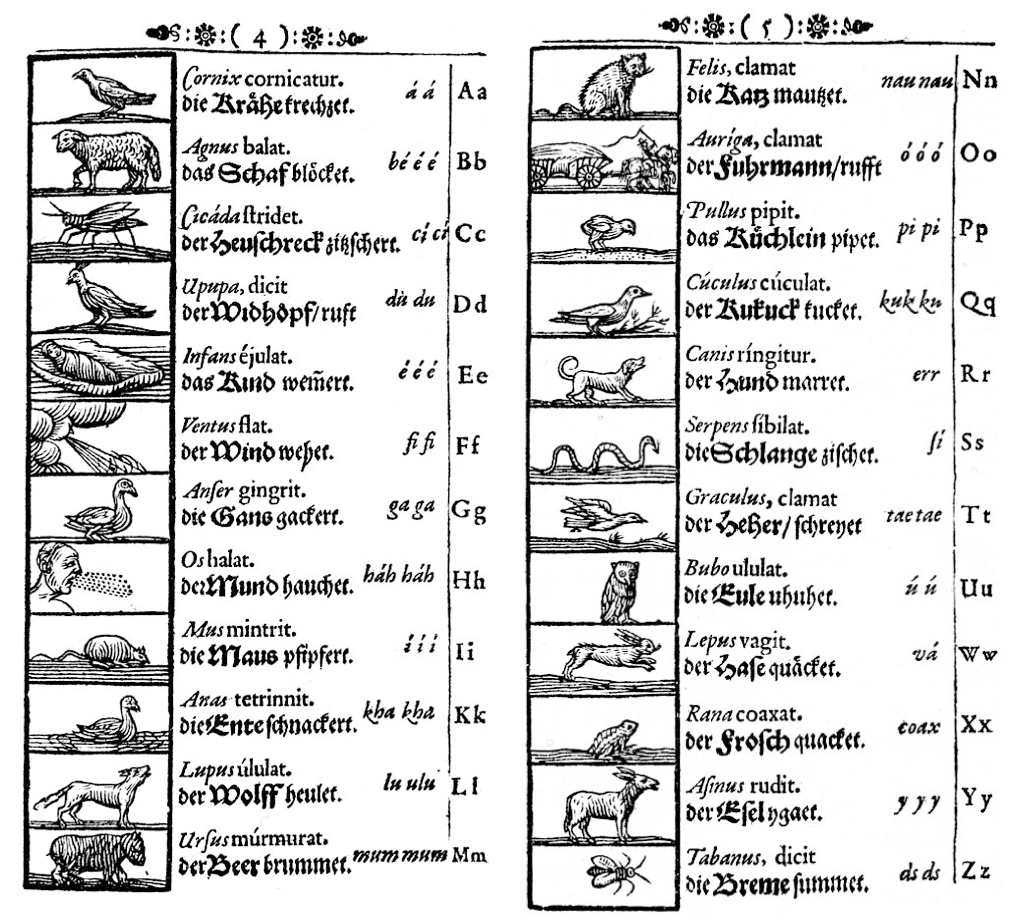As scholar Whitney Trettien writes:
“[T]he Orbis Pictus renders the alphabet’s arbitrary arrangement and strange relationship with sound as… a reflection of the natural, divine order…. [L]earning the alphabet becomes a process of learning God’s creation. […] [T]o read a word simply is to write — and right — the universe, as the material manipulation of a finite set (the 26 letters) unlocks the infinite multitude of God’s creation.”11
In other words: although the alphabet’s arrangement is arbitrary, contingent, an accident of history, works like this “retcon” the order of the alphabet to actually mean something. In the process, they mistake the (arbitrary) order of the alphabet for the order of the world. The alphabet ends up being weird fertilizer for this kind of abstract metaphysics—mistaking the map for the territory on a grand scale. This (faulty) equation of alphabetical knowledge with arcane understanding of the world may also be the source of the outsized social status we tend to confer to “good” spelling (or good Scrabble scores).
Don’t get me wrong—the alphabet is actually an amazing abstraction. More than any writing system, it allows for the most direct relationship between sound and symbol, which leads to remarkable expressiveness in the form of non-standard spelling. It’s the only kind of writing system that is essentially completely linear with no hierarchical organization inside of the glyphs themselves, and therefore more amenable to digital representation. (In a workshop recently, Philosopher Alex Galloway called the alphabet “the killer app of digitality.”)
I call this idea—i.e., that the alphabet and language are the same thing—the “alphabet fetish.” And it leads to very weird misunderstandings, like this one: if I asked you how many vowels there are in English, what would you answer? In my experience, most English speakers answer this question with “five”—a, e, i, o, u. (“And sometimes y,” someone inevitably adds.)
In fact, English has at least ten vowels, and potentially as many as fourteen, depending on the variety of English you’re speaking and whether or not you could diphthongs as distinct vowels (or compositions of their constituent vowels). How do we know this? As an exercise, consider this list:
teak, tick, take, tech, tack, talk, toke, took, tuque (a knit cap in Canada), tuck, Turk, tyke
Read this list out loud and don’t pay attention to the spelling. You’ll find that the first and last consonant of each of these words is the same (“T” and “K”), and only the sound between them is different. Depending on your accent, you’ll find that each of these words sounds different from all the others, based solely on the distinct vowel sound. That means that we must have at least twelve distinct vowels in English, regardless of the number of letters we use to write those vowels.
It’s fairly unusual for languages to have this many distinctive vowels. (For example, most varieties of Spanish have only five distinctive vowels.) The “alphabet fetish,” in this case, is making a fascinating, beautiful aspect of english invisible—in people’s minds, the abstraction overrides reality.
Rewordable, of course, is still based on the alphabet. But the game does break down language differently from other spelling games—the primary unit is the sequence, not the individual letter. One of the ideas I was trying to incorporate into Rewordable from the beginning is that the alphabet is arbitrary. Here are two diagrams illustrating different models of understanding language. On the left is the “alphabet fetish” model, in which language is a sort of degenerate form of the alphabet. On the right is a model of the understanding I’m trying to argue for as a poet/linguist/game designer/whatever:
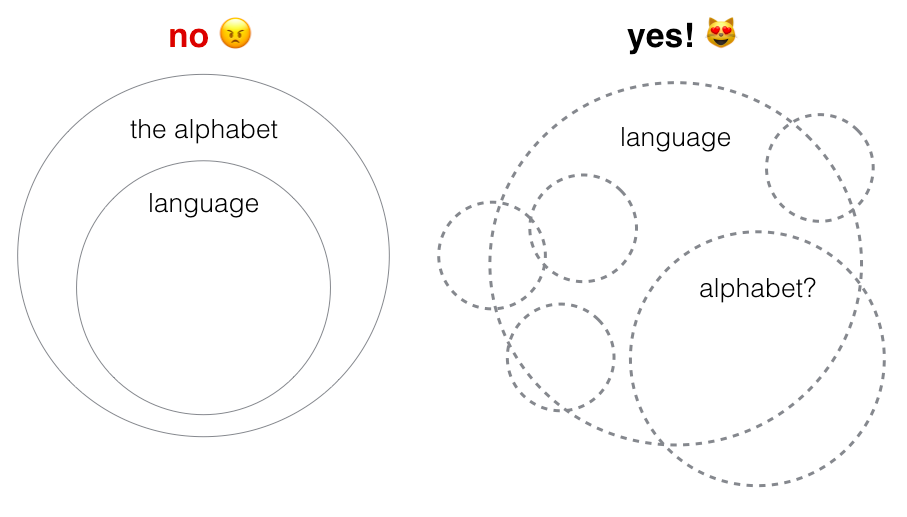What I want people to understand is that language has a porous conceptual border; you can’t draw a circle around it. The alphabet is one possible way of breaking a language into units, but it’s not the only one. (Sorry, Erigena.)
Let’s return to the axiom. On further reflection, I realized there are all kinds of propositions that the axiom either presupposes or implies, which I’ve outlined below. Scrabble is very strenuously argues for all of these things, and what I’m realizing is that I find spelling games interesting to the extent that they violate one or more of these secondary axioms. This is my list of rules to throw in the trash for my next spelling game, feel free to borrow them:
So here are the takeaways: what I learned from co-designing Rewordable.
After all that, I want to come back to the social media message that I started with. Is Rewordable just “Scrabble meets Bananagrams”? Let’s see what the players have to say about it.
These reviews from Amazon seem to indicate we managed to make something that feels different! “Every combination of cards is a challenge you haven’t seen before,” writes one. “Easier for kids to make words, and it can help change their way of thinking,” writes another. Most importantly, “it offers something unlike Scrabble or Bananagrams.” Yesss. Take that, sales and marketing.
Alfred Mosher Butts, ca. 1933, as quoted in Fatsis, Stefan. Word Freak: Heartbreak, Triumph, Genius, and Obsession in the World of Competitive Scrabble Players. HMH, 2001, pp. 92–93.↩︎
Fatsis, Stefan. “What’s a Z Really Worth?”. Slate, Jan. 2013. Slate, http://www.slate.com/articles/sports/gaming/2013/01/scrabble_tile_values_why_it_s_a_mistake_to_change_the_point_value_of_the.html.↩︎
Smith, Ernie. “The ABCs of Wooden Alphabet Blocks.” Atlas Obscura, 23 May 2017, http://www.atlasobscura.com/articles/history-alphabet-blocks.↩︎
Image source, which also has a very good description of the game itself.↩︎
Poe, Edgar Allan. The Gold Bug. G. Routledge & Sons, Limited, 1891, p. 100.↩︎
Fatsis, Word Freak, p. 92.↩︎
Friedman, William F. “Edgar Allan Poe, Cryptographer.” On Poe, edited by Louis J. Budd and Edwin Harrison Cady, Duke University Press, 1993, pp. 40–54.↩︎
Al-Kadit, Ibrahim A. “Origins of Cryptology: The Arab Contributions.” Cryptologia, vol. 16, no. 2, Apr. 1992, pp. 97–126.↩︎
Quoted in Leggott, Michele J. Reading Zukofsky’s 80 Flowers. Johns Hopkins Univ Press, 1989, p. 46.↩︎
Trettien, Whitney Anne. Computers, Cut-Ups and Combinatory Volvelles: An Archaeology of Text-Generating Mechanisms. MIT, 2009, http://whitneyannetrettien.com/thesis/, lexia 4622–4623.↩︎